gghistostats

Indrajeet Patil

2022-09-03

---

You can cite this package/vignette as:

To cite package 'ggstatsplot' in publications use:

  Patil, I. (2021). Visualizations with statistical details: The
  'ggstatsplot' approach. Journal of Open Source Software, 6(61), 3167,
  doi:10.21105/joss.03167

A BibTeX entry for LaTeX users is

  @Article{,
    doi = {10.21105/joss.03167},
    url = {https://doi.org/10.21105/joss.03167},
    year = {2021},
    publisher = {{The Open Journal}},
    volume = {6},
    number = {61},
    pages = {3167},
    author = {Indrajeet Patil},
    title = {{Visualizations with statistical details: The {'ggstatsplot'} approach}},
    journal = {{Journal of Open Source Software}},
  }

---

Lifecycle:

The function gghistostats can be used for data exploration and to provide an easy way to make publication-ready histograms with appropriate and selected statistical details embedded in the plot itself. In this vignette we will explore several examples of how to use it.

Some instances where you would want to use gghistostats-

• to inspect distribution of a continuous variable
• to test if the mean of a sample variable is different from a specified value (population parameter)

Statistical analysis with gghistostats

Let’s begin with a very simple example from the psych package (psych::sat.act), a sample of 700 self-reported scores on the SAT Verbal, SAT Quantitative and ACT tests. ACT composite scores may range from 1 - 36. National norms have a mean of 20.

## loading needed libraries
library(ggstatsplot)
library(psych)
library(dplyr)

## looking at the structure of the data using glimpse
dplyr::glimpse(psych::sat.act)
#> Rows: 700
#> Columns: 6
#> $ gender    <int> 2, 2, 2, 1, 1, 1, 2, 1, 2, 2, 1, 2, 1, 2, 2, 2, 2, 2, 1, 2, …
#> $ education <int> 3, 3, 3, 4, 2, 5, 5, 3, 4, 5, 3, 4, 4, 4, 3, 4, 3, 4, 4, 4, …
#> $ age       <int> 19, 23, 20, 27, 33, 26, 30, 19, 23, 40, 23, 34, 32, 41, 20, …
#> $ ACT       <int> 24, 35, 21, 26, 31, 28, 36, 22, 22, 35, 32, 29, 21, 35, 27, …
#> $ SATV      <int> 500, 600, 480, 550, 600, 640, 610, 520, 400, 730, 760, 710, …
#> $ SATQ      <int> 500, 500, 470, 520, 550, 640, 500, 560, 600, 800, 710, 600, …

To get a simple histogram with no statistics and no special information. gghistostats will by default choose a binwidth max(x) - min(x) / sqrt(N). You should always check this value and explore multiple widths to find the best to illustrate the stories in your data since histograms are sensitive to binwidth.

Let’s display the national norms (labeled as “Test”) and test the hypothesis that our sample mean is the same as our national population mean of 20 using a parametric one sample t-test (type = "p").

set.seed(123)

gghistostats(
  data = psych::sat.act, ## data from which variable is to be taken
  x = ACT, ## numeric variable
  xlab = "ACT Score", ## x-axis label
  title = "Distribution of ACT Scores", ## title for the plot
  test.value = 20, ## test value
  caption = "Data courtesy of: SAPA project (https://sapa-project.org)"
)

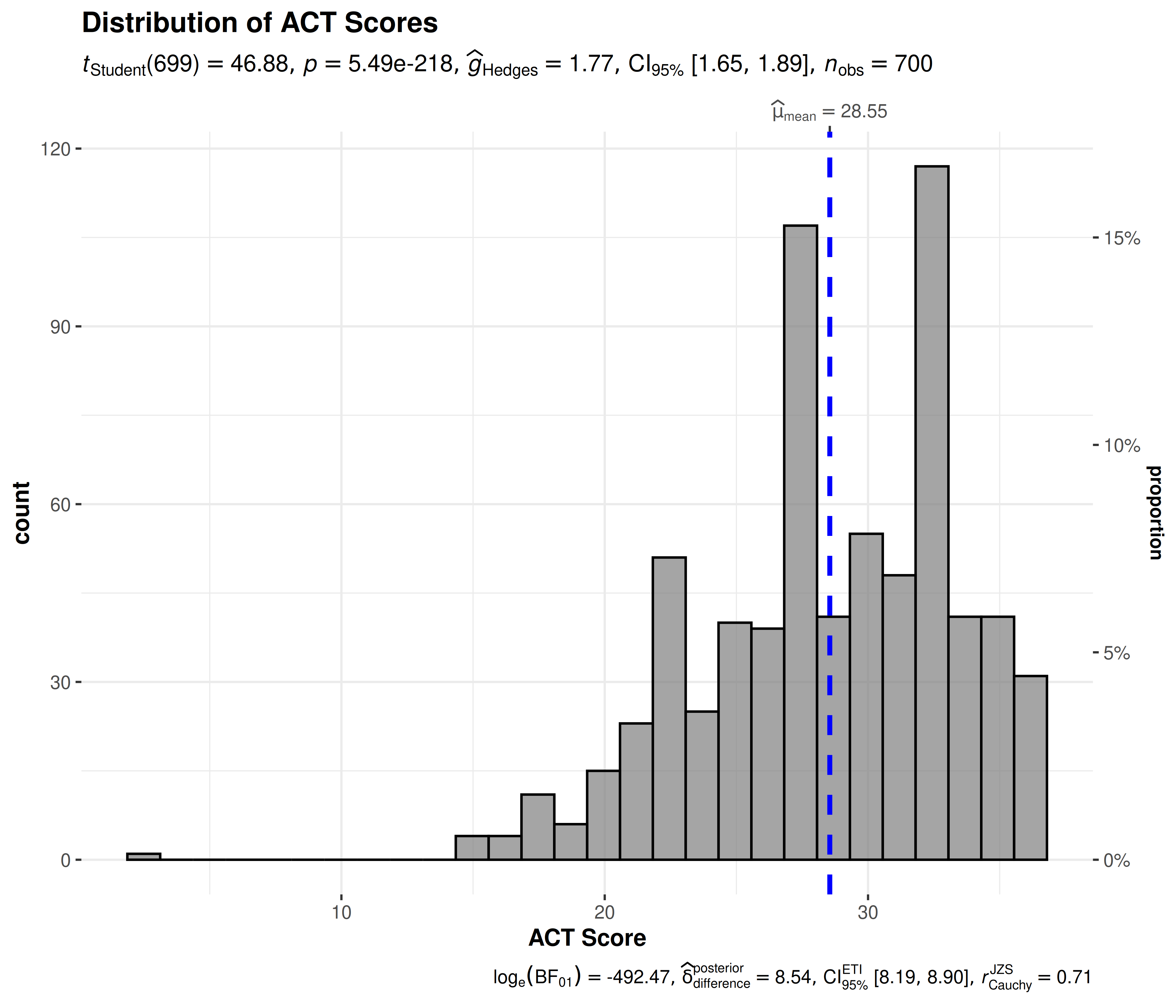
gghistostats computed Bayes Factors to quantify the likelihood of the research (BF10) and the null hypothesis (BF01). In our current example, the Bayes Factor value provides very strong evidence (Kass and Rafferty, 1995) in favor of the research hypothesis: these ACT scores are much higher than the national average. The log(Bayes factor) of 492.5 means the odds are 7.54e+213:1 that this sample is different.

Grouped analysis with grouped_gghistostats

What if we want to do the same analysis separately for each gender? ggstatsplot provides a special helper function for such instances: grouped_gghistostats. This is merely a wrapper function around combine_plots. It applies gghistostats across all levels of a specified grouping variable and then combines the individual plots into a single plot. Note that the grouping variable can be anything: conditions in a given study, groups in a study sample, different studies, etc.

Let’s see how we can use this function to apply gghistostats to accomplish our task.

set.seed(123)

grouped_gghistostats(
  ## arguments relevant for gghistostats
  data = psych::sat.act,
  x = ACT, ## same outcome variable
  xlab = "ACT Score",
  grouping.var = gender, ## grouping variable males = 1, females = 2
  type = "robust", ## robust test: one-sample percentile bootstrap
  test.value = 20, ## test value against which sample mean is to be compared
  centrality.line.args = list(color = "#D55E00", linetype = "dashed"),
  # ggtheme = ggthemes::theme_stata(), ## changing default theme
  ## turn off ggstatsplot theme layer
  ## arguments relevant for combine_plots
  annotation.args = list(
    title = "Distribution of ACT scores across genders",
    caption = "Data courtesy of: SAPA project (https://sapa-project.org)"
  ),
  plotgrid.args = list(nrow = 2)
)

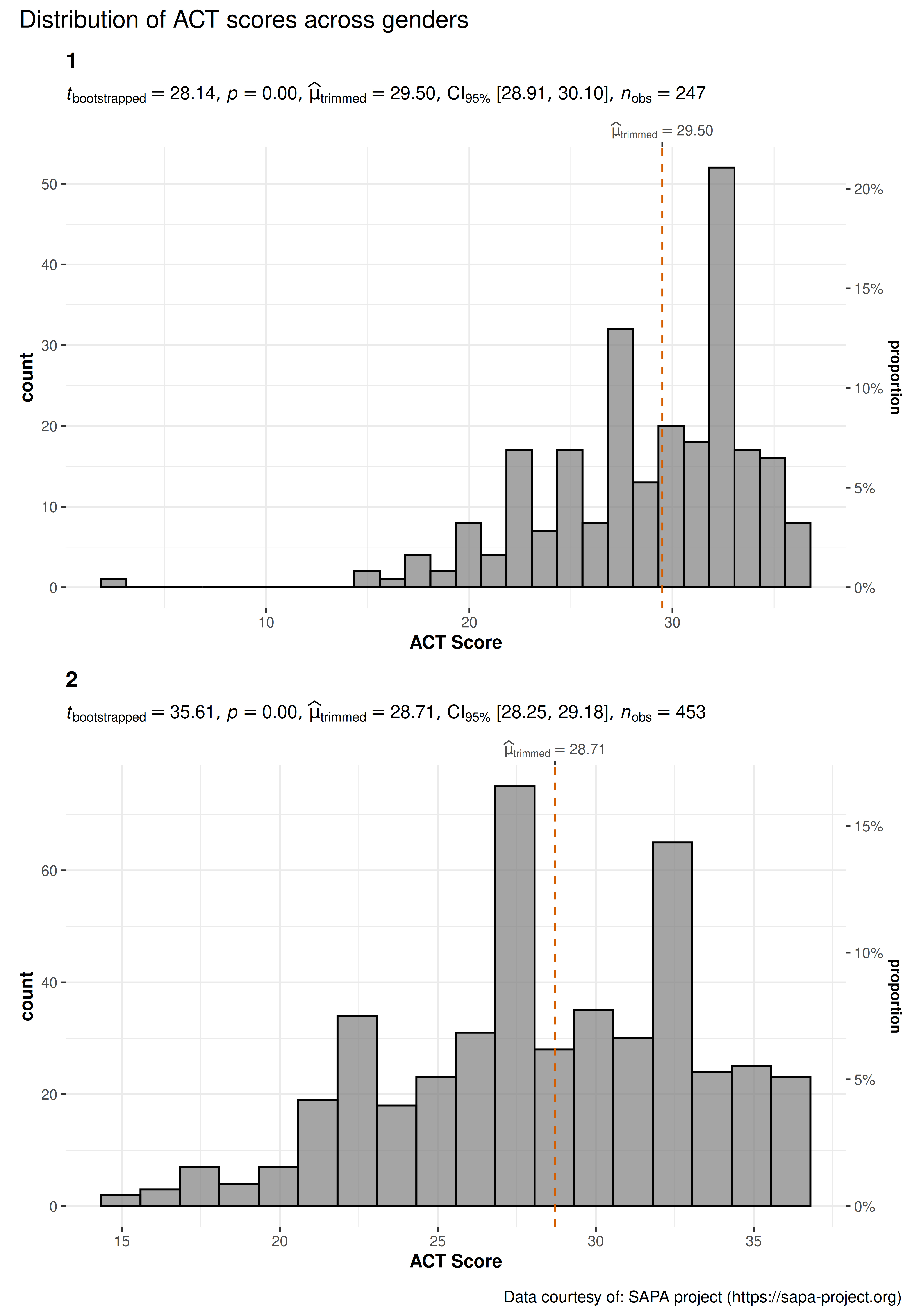
As can be seen from these plots, the mean value is much higher than the national norm. Additionally, we see the benefits of plotting this data separately for each gender. We can see the differences in distributions.

Grouped analysis with {purrr}

Although this is a quick and dirty way to explore a large amount of data with minimal effort, it does come with an important limitation: reduced flexibility. For example, if we wanted to add, let’s say, a separate test.value argument for each gender, this is not possible with grouped_gghistostats.

For cases like these, or to run separate kinds of tests (robust for some, parametric for other, while Bayesian for some other levels of the group) it would be better to use purrr.

See the associated vignette here: https://indrajeetpatil.github.io/ggstatsplot/articles/web_only/purrr_examples.html

Summary of graphics

graphical element	geom_ used	argument for further modification
histogram bin	ggplot2::stat_bin	bin.args
centrality measure line	ggplot2::geom_vline	centrality.line.args
normality curve	ggplot2::stat_function	normal.curve.args

Summary of tests

Central tendency measure

Type	Measure	Function used
Parametric	mean	datawizard::describe_distribution
Non-parametric	median	datawizard::describe_distribution
Robust	trimmed mean	datawizard::describe_distribution
Bayesian	MAP (maximum a posteriori probability) estimate	datawizard::describe_distribution

Hypothesis testing

Type	Test	Function used
Parametric	One-sample Student’s t-test	stats::t.test
Non-parametric	One-sample Wilcoxon test	stats::wilcox.test
Robust	Bootstrap-t method for one-sample test	WRS2::trimcibt
Bayesian	One-sample Student’s t-test	BayesFactor::ttestBF

Effect size estimation

Type	Effect size	CI?	Function used
Parametric	Cohen’s d, Hedge’s g	✅	effectsize::cohens_d, effectsize::hedges_g
Non-parametric	r (rank-biserial correlation)	✅	effectsize::rank_biserial
Robust	trimmed mean	✅	WRS2::trimcibt
Bayes Factor	\(\delta_{posterior}\)	✅	bayestestR::describe_posterior

Reporting

If you wish to include statistical analysis results in a publication/report, the ideal reporting practice will be a hybrid of two approaches:

• the ggstatsplot approach, where the plot contains both the visual and numerical summaries about a statistical model, and

• the standard narrative approach, which provides interpretive context for the reported statistics.

For example, let’s see the following example:

gghistostats(trees, Height, test.value = 75)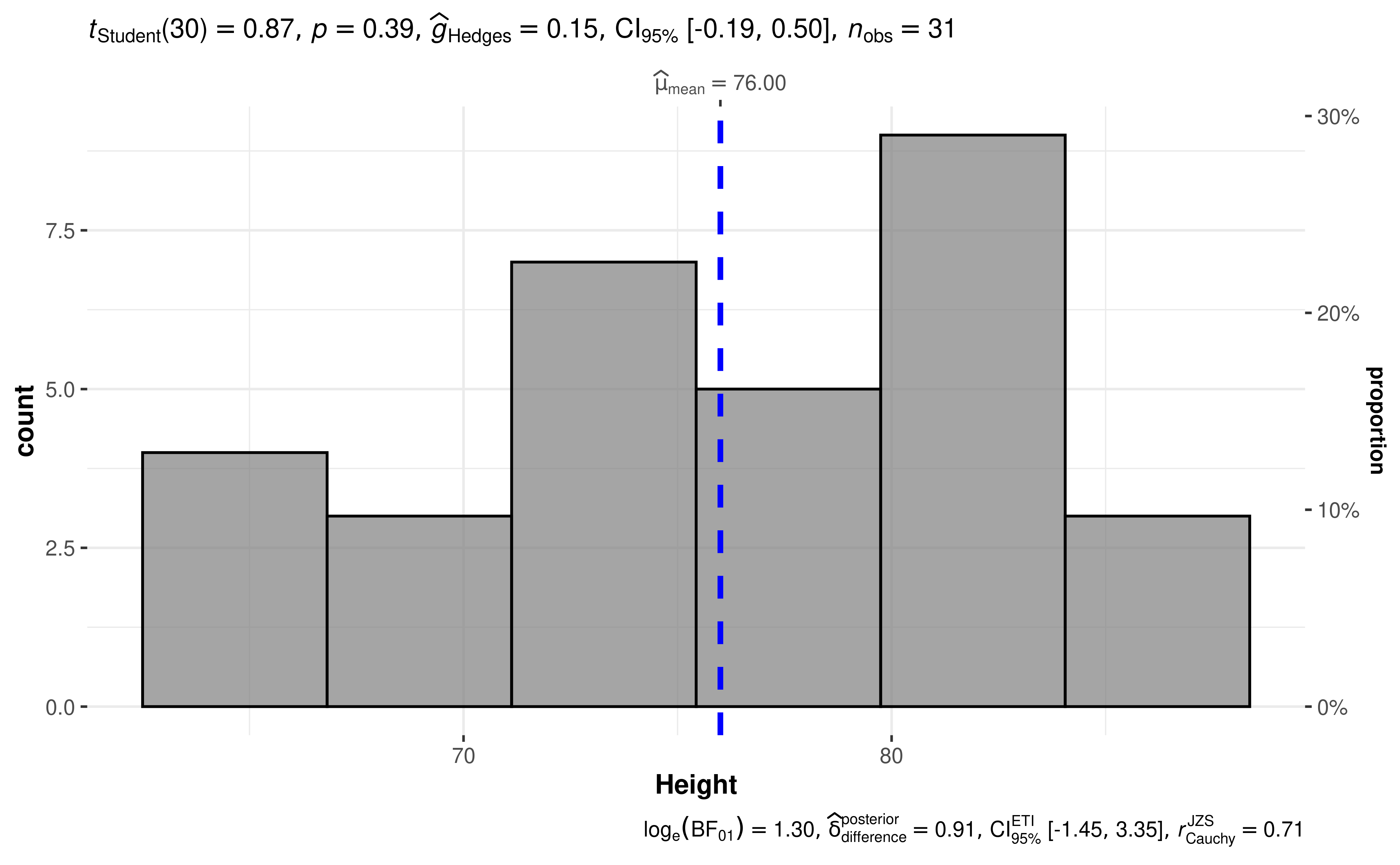

The narrative context (assuming type = "parametric") can complement this plot either as a figure caption or in the main text-

Student’s t-test revealed that, across 31 felled black cherry trees, although the height was higher than expected height of 75 ft., this effect was not statistically significant. The effect size \((g = 0.15)\) was small, as per Cohen’s (1988) conventions. The Bayes Factor for the same analysis revealed that the data were 3.67 times more probable under the null hypothesis as compared to the alternative hypothesis. This can be considered moderate evidence (Jeffreys, 1961) in favor of the null hypothesis.

Suggestions

If you find any bugs or have any suggestions/remarks, please file an issue on GitHub: https://github.com/IndrajeetPatil/ggstatsplot/issues