You can cite this package/vignette as:
To cite package 'ggstatsplot' in publications use:
Patil, I. (2021). Visualizations with statistical details: The
'ggstatsplot' approach. Journal of Open Source Software, 6(61), 3167,
doi:10.21105/joss.03167
A BibTeX entry for LaTeX users is
@Article{,
doi = {10.21105/joss.03167},
url = {https://doi.org/10.21105/joss.03167},
year = {2021},
publisher = {{The Open Journal}},
volume = {6},
number = {61},
pages = {3167},
author = {Indrajeet Patil},
title = {{Visualizations with statistical details: The {'ggstatsplot'} approach}},
journal = {{Journal of Open Source Software}},
}The function ggbetweenstats is designed to facilitate
data exploration, and for making highly customizable
publication-ready plots, with relevant statistical
details included in the plot itself if desired. We will see examples of
how to use this function in this vignette.
To begin with, here are some instances where you would want to use
ggbetweenstats-
to check if a continuous variable differs across multiple groups/conditions
to compare distributions visually
Note: This vignette uses the pipe operator
(%>%), if you are not familiar with this operator, here
is a good explanation: http://r4ds.had.co.nz/pipes.html
Comparisons between groups with ggbetweenstats
To illustrate how this function can be used, we will use the
gapminder dataset throughout this vignette. This dataset
provides values for life expectancy, GDP per capita, and population, at
5 year intervals, from 1952 to 2007, for each of 142 countries (courtesy
Gapminder Foundation). Let’s
have a look at the data-
library(gapminder)
dplyr::glimpse(gapminder::gapminder)
#> Rows: 1,704
#> Columns: 6
#> $ country <fct> "Afghanistan", "Afghanistan", "Afghanistan", "Afghanistan", …
#> $ continent <fct> Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, Asia, …
#> $ year <int> 1952, 1957, 1962, 1967, 1972, 1977, 1982, 1987, 1992, 1997, …
#> $ lifeExp <dbl> 28.801, 30.332, 31.997, 34.020, 36.088, 38.438, 39.854, 40.8…
#> $ pop <int> 8425333, 9240934, 10267083, 11537966, 13079460, 14880372, 12…
#> $ gdpPercap <dbl> 779.4453, 820.8530, 853.1007, 836.1971, 739.9811, 786.1134, …Note: For the remainder of the vignette, we’re going to exclude Oceania from the analysis simply because there are so few observations (countries).
Suppose the first thing we want to inspect is the distribution of life expectancy for the countries of a continent in 2007. We also want to know if the mean differences in life expectancy between the continents is statistically significant.
The simplest form of the function call is-
ggbetweenstats(
data = dplyr::filter(gapminder::gapminder, year == 2007, continent != "Oceania"),
x = continent,
y = lifeExp
)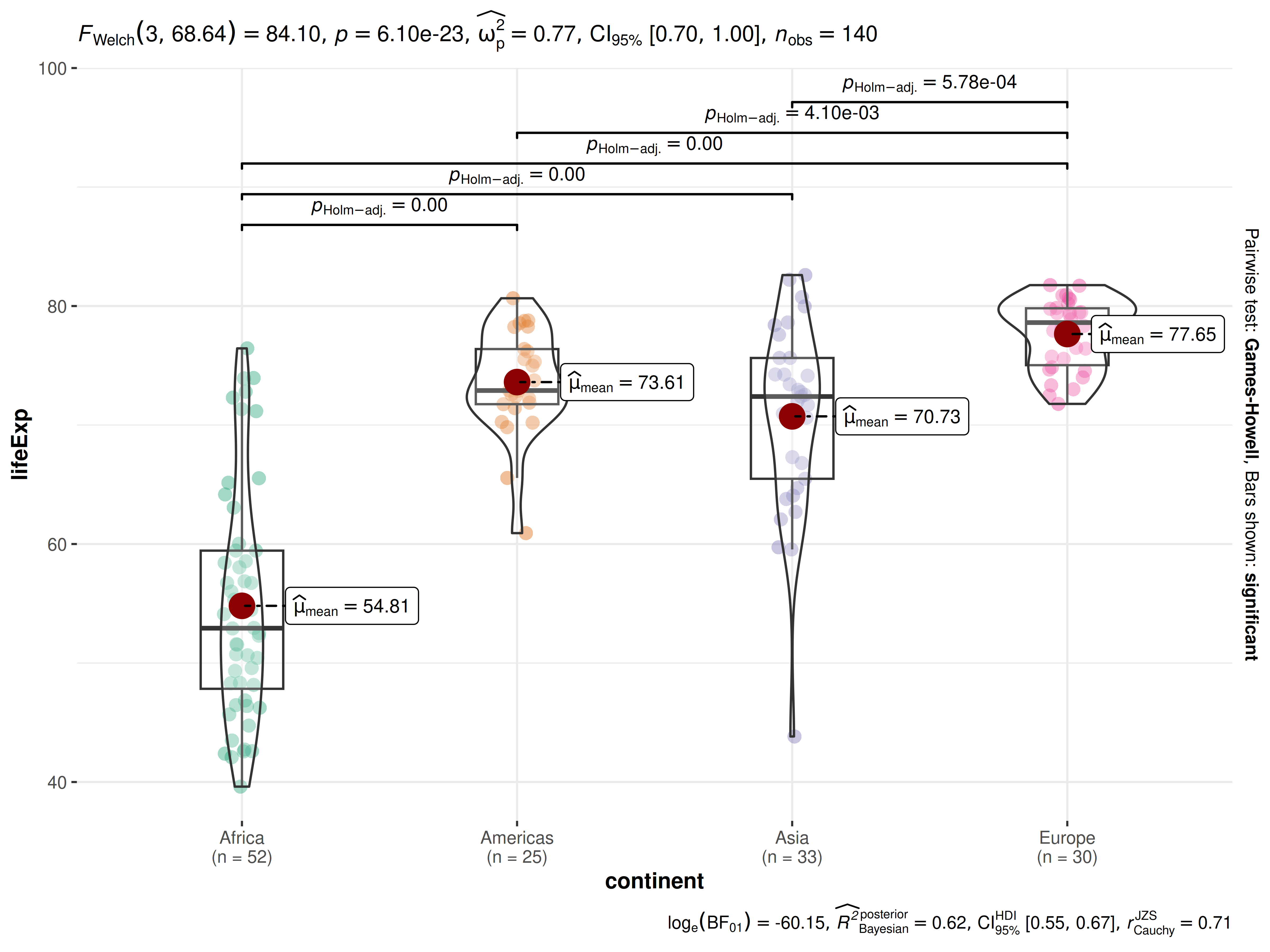
Note:
The function automatically decides whether an independent samples t-test is preferred (for 2 groups) or a Oneway ANOVA (3 or more groups). based on the number of levels in the grouping variable.
The output of the function is a
ggplotobject which means that it can be further modified with ggplot2 functions.
As can be seen from the plot, the function by default returns Bayes Factor for the test. If the null hypothesis can’t be rejected with the null hypothesis significance testing (NHST) approach, the Bayesian approach can help index evidence in favor of the null hypothesis (i.e., ).
By default, natural logarithms are shown because Bayes Factor values can sometimes be pretty large. Having values on logarithmic scale also makes it easy to compare evidence in favor alternative () versus null () hypotheses (since ).
We can make the output much more aesthetically pleasing as well as
informative by making use of the many optional parameters in
ggbetweenstats. We’ll add a title and caption, better
x and y axis labels. We can and will change
the overall theme as well as the color palette in use.
ggbetweenstats(
data = dplyr::filter(gapminder, year == 2007, continent != "Oceania"),
x = continent, ## grouping/independent variable
y = lifeExp, ## dependent variables
type = "robust", ## type of statistics
xlab = "Continent", ## label for the x-axis
ylab = "Life expectancy", ## label for the y-axis
## turn off messages
ggtheme = ggplot2::theme_gray(), ## a different theme
package = "yarrr", ## package from which color palette is to be taken
palette = "info2", ## choosing a different color palette
title = "Comparison of life expectancy across continents (Year: 2007)",
caption = "Source: Gapminder Foundation"
) + ## modifying the plot further
ggplot2::scale_y_continuous(
limits = c(35, 85),
breaks = seq(from = 35, to = 85, by = 5)
)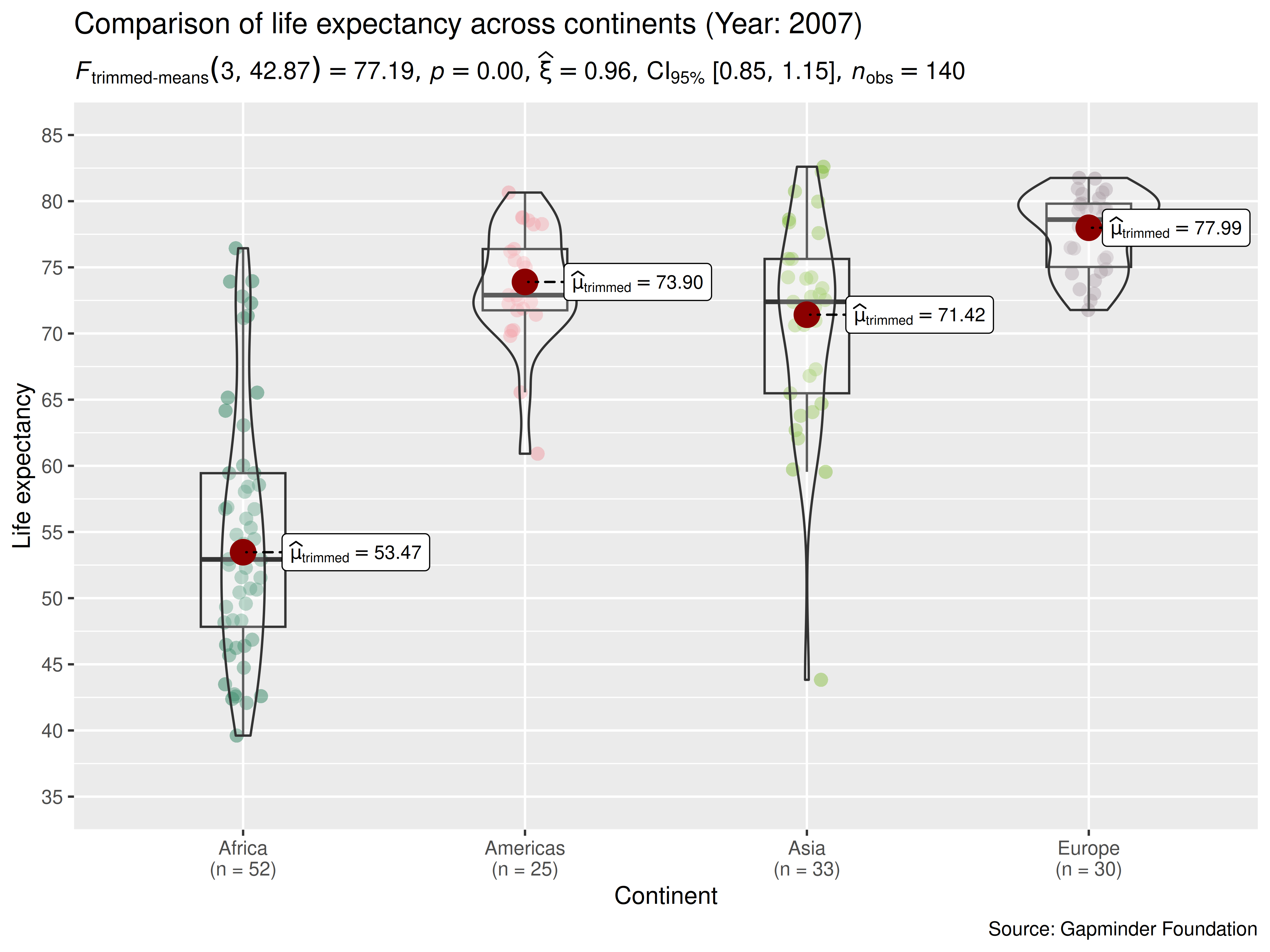
As can be appreciated from the effect size (partial eta squared) of 0.635, there are large differences in the mean life expectancy across continents. Importantly, this plot also helps us appreciate the distributions within any given continent. For example, although Asian countries are doing much better than African countries, on average, Afghanistan has a particularly grim average for the Asian continent, possibly reflecting the war and the political turmoil.
So far we have only used a classic parametric test and a boxviolin plot, but we can also use other available options:
The
type(of test) argument also accepts the following abbreviations:"p"(for parametric),"np"(for nonparametric),"r"(for robust),"bf"(for Bayes Factor).The type of plot to be displayed can also be modified (
"box","violin", or"boxviolin").The color palettes can be modified.
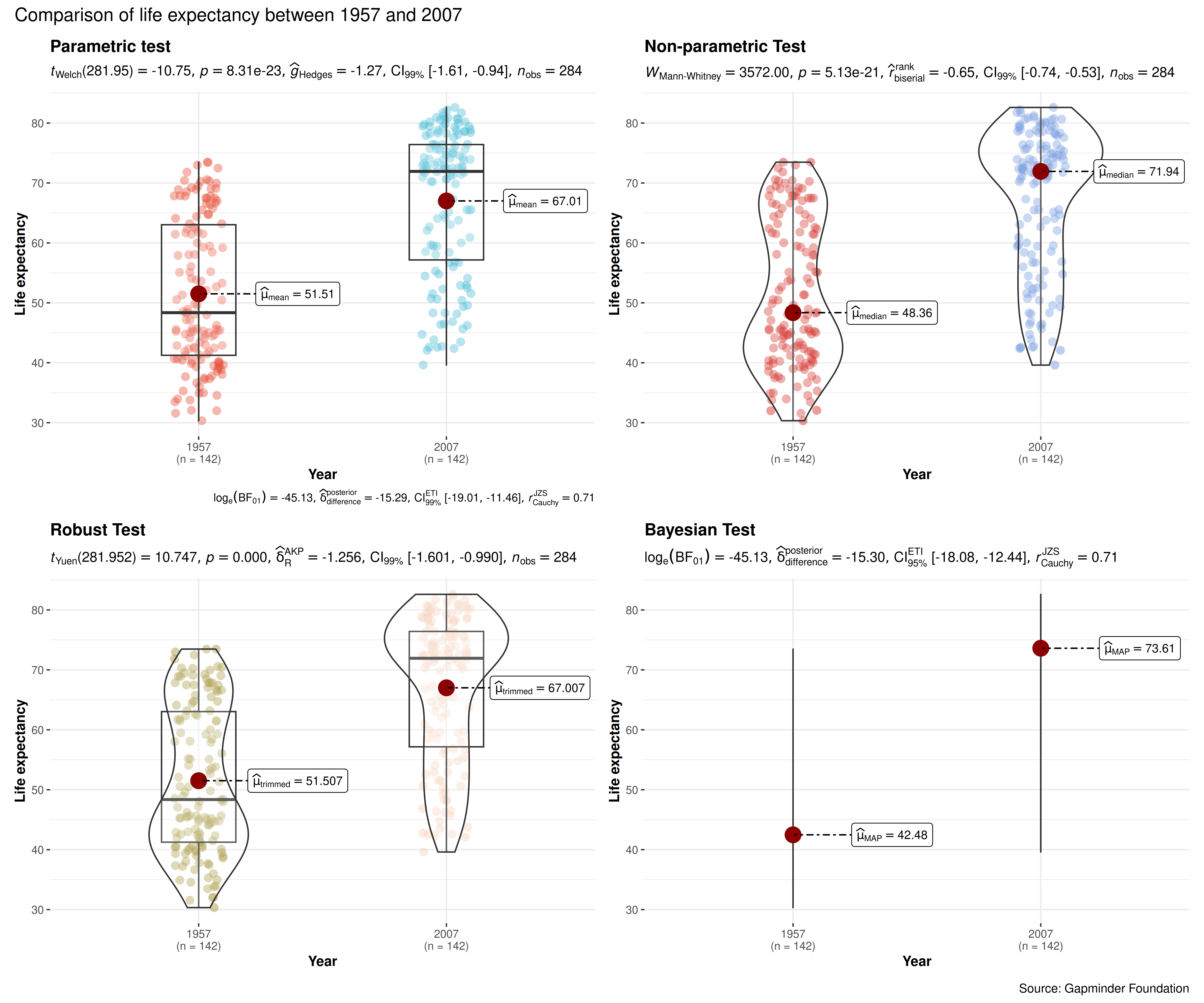
Let’s use the combine_plots function to make one plot
from four separate plots that demonstrates all of these options. Let’s
compare life expectancy for all countries for the first and last year of
available data 1957 and 2007. We will generate the plots one by one and
then use combine_plots to merge them into one plot with
some common labeling. It is possible, but not necessarily recommended,
to make each plot have different colors or themes.
For example,
## selecting subset of the data
df_year <- dplyr::filter(gapminder::gapminder, year == 2007 | year == 1957)
p1 <- ggbetweenstats(
data = df_year,
x = year,
y = lifeExp,
xlab = "Year",
ylab = "Life expectancy",
# to remove violin plot
violin.args = list(width = 0),
type = "p",
conf.level = 0.99,
title = "Parametric test",
package = "ggsci",
palette = "nrc_npg"
)
p2 <- ggbetweenstats(
data = df_year,
x = year,
y = lifeExp,
xlab = "Year",
ylab = "Life expectancy",
# to remove box plot
boxplot.args = list(width = 0),
type = "np",
conf.level = 0.99,
title = "Non-parametric Test",
package = "ggsci",
palette = "uniform_startrek"
)
p3 <- ggbetweenstats(
data = df_year,
x = year,
y = lifeExp,
xlab = "Year",
ylab = "Life expectancy",
type = "r",
conf.level = 0.99,
title = "Robust Test",
tr = 0.005,
package = "wesanderson",
palette = "Royal2",
digits = 3
)
## Bayes Factor for parametric t-test and boxviolin plot
p4 <- ggbetweenstats(
data = df_year,
x = year,
y = lifeExp,
xlab = "Year",
ylab = "Life expectancy",
type = "bayes",
violin.args = list(width = 0),
boxplot.args = list(width = 0),
point.args = list(alpha = 0),
title = "Bayesian Test",
package = "ggsci",
palette = "nrc_npg"
)
## combining the individual plots into a single plot
combine_plots(
list(p1, p2, p3, p4),
plotgrid.args = list(nrow = 2L),
annotation.args = list(
title = "Comparison of life expectancy between 1957 and 2007",
caption = "Source: Gapminder Foundation"
)
)
Grouped analysis with grouped_ggbetweenstats
What if we want to analyze both by continent and between 1957 and 2007? A combination of our two previous efforts.
ggstatsplot provides a special helper function for
such instances: grouped_ggbetweenstats. This is merely a
wrapper function around combine_plots. It applies
ggbetweenstats across all levels of a
specified grouping variable and then combines list of
individual plots into a single plot. Note that the grouping variable can
be anything: conditions in a given study, groups in a study sample,
different studies, etc.
Let’s focus on the same 4 continents for the following years: 1967, 1987, 2007. Also, let’s carry out pairwise comparisons to see if there differences between every pair of continents.
## select part of the dataset and use it for plotting
gapminder::gapminder %>%
dplyr::filter(year %in% c(1967, 1987, 2007), continent != "Oceania") %>%
grouped_ggbetweenstats(
## arguments relevant for ggbetweenstats
x = continent,
y = lifeExp,
grouping.var = year,
xlab = "Continent",
ylab = "Life expectancy",
pairwise.display = "significant", ## display only significant pairwise comparisons
p.adjust.method = "fdr", ## adjust p-values for multiple tests using this method
# ggtheme = ggthemes::theme_tufte(),
package = "ggsci",
palette = "default_jco",
## arguments relevant for combine_plots
annotation.args = list(title = "Changes in life expectancy across continents (1967-2007)"),
plotgrid.args = list(nrow = 3)
)
As seen from the plot, although the life expectancy has been improving steadily across all continents as we go from 1967 to 2007, this improvement has not been happening at the same rate for all continents. Additionally, irrespective of which year we look at, we still find significant differences in life expectancy across continents which have been surprisingly consistent across five decades (based on the observed effect sizes).
Grouped analysis with ggbetweenstats +
{purrr}
Although this grouping function provides a quick way to explore the
data, it leaves much to be desired. For example, the same type of plot
and test is applied for all years, but maybe we want to change this for
different years, or maybe we want to gave different effect sizes for
different years. This type of customization for different levels of a
grouping variable is not possible with
grouped_ggbetweenstats, but this can be easily achieved
using the purrr package.
See the associated vignette here: https://indrajeetpatil.github.io/ggstatsplot/articles/web_only/purrr_examples.html
Within-subjects designs
For repeated measures designs, ggwithinstats() function
can be used: https://indrajeetpatil.github.io/ggstatsplot/articles/web_only/ggwithinstats.html
Summary of graphics and tests
Details about underlying functions used to create graphics and statistical tests carried out can be found in the function documentation: https://indrajeetpatil.github.io/ggstatsplot/reference/ggbetweenstats.html
Reporting
If you wish to include statistical analysis results in a publication/report, the ideal reporting practice will be a hybrid of two approaches:
the ggstatsplot approach, where the plot contains both the visual and numerical summaries about a statistical model, and
the standard narrative approach, which provides interpretive context for the reported statistics.
For example, let’s see the following example:
ggbetweenstats(ToothGrowth, supp, len)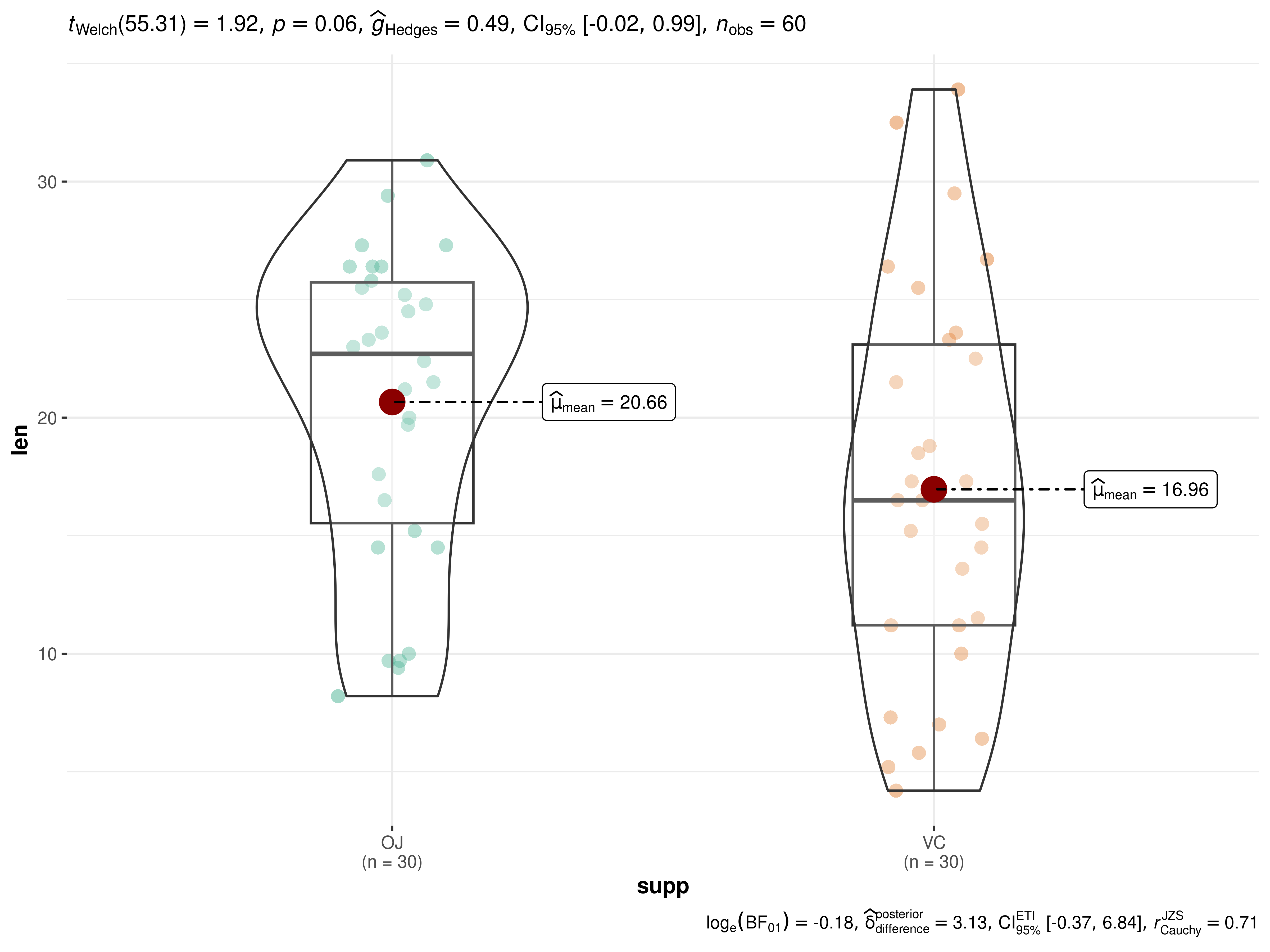
The narrative context (assuming type = "parametric") can
complement this plot either as a figure caption or in the main text-
Welch’s t-test revealed that, across 60 guinea pigs, although the tooth length was higher when the animal received vitamin C via orange juice as compared to via ascorbic acid, this effect was not statistically significant. The effect size was medium, as per Cohen’s (1988) conventions. The Bayes Factor for the same analysis revealed that the data were 1.2 times more probable under the alternative hypothesis as compared to the null hypothesis. This can be considered weak evidence (Jeffreys, 1961) in favor of the alternative hypothesis.
Similar reporting style can be followed when the function performs one-way ANOVA instead of a t-test.
Suggestions
If you find any bugs or have any suggestions/remarks, please file an
issue on GitHub: https://github.com/IndrajeetPatil/ggstatsplot/issues

