24 Improving performance
Attaching the needed libraries:
24.1 Exercises 24.3.1
Q1. What are faster alternatives to lm()? Which are specifically designed to work with larger datasets?
A1. Faster alternatives to lm() can be found by visiting CRAN Task View: High-Performance and Parallel Computing with R page.
Here are some of the available options:
speedglm::speedlm()(for large datasets)biglm::biglm()(specifically designed for data too large to fit in memory)RcppEigen::fastLm()(using theEigenlinear algebra library)
High performances can be obtained with these packages especially if R is linked against an optimized BLAS, such as ATLAS. You can check this information using sessionInfo():
sessInfo <- sessionInfo()
sessInfo$matprod
#> [1] "default"
sessInfo$LAPACK
#> [1] "/usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.26.so"Comparing performance of different alternatives:
library(gapminder)
# having a look at the data
glimpse(gapminder)
#> Rows: 1,704
#> Columns: 6
#> $ country <fct> "Afghanistan", "Afghanistan", "Afghanist…
#> $ continent <fct> Asia, Asia, Asia, Asia, Asia, Asia, Asia…
#> $ year <int> 1952, 1957, 1962, 1967, 1972, 1977, 1982…
#> $ lifeExp <dbl> 28.801, 30.332, 31.997, 34.020, 36.088, …
#> $ pop <int> 8425333, 9240934, 10267083, 11537966, 13…
#> $ gdpPercap <dbl> 779.4453, 820.8530, 853.1007, 836.1971, …
bench::mark(
"lm" = stats::lm(lifeExp ~ continent * gdpPercap, gapminder),
"speedglm" = speedglm::speedlm(lifeExp ~ continent * gdpPercap, gapminder),
"biglm" = biglm::biglm(lifeExp ~ continent * gdpPercap, gapminder),
"fastLm" = RcppEigen::fastLm(lifeExp ~ continent * gdpPercap, gapminder),
check = FALSE,
iterations = 1000
)[1:5]
#> # A tibble: 4 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 lm 883.03µs 932.73µs 1064. 1.18MB
#> 2 speedglm 1.08ms 1.15ms 766. 71MB
#> 3 biglm 815.03µs 855.7µs 1149. 589.43KB
#> 4 fastLm 1.01ms 1.04ms 953. 4.6MBThe results might change depending on the size of the dataset, with the performance benefits accruing bigger the dataset.
You will have to experiment with different algorithms and find the one that fits the needs of your dataset the best.
Q2. What package implements a version of match() that’s faster for repeated look ups? How much faster is it?
A2. The package (and the respective function) is fastmatch::fmatch()7.
The documentation for this function notes:
It is slightly faster than the built-in version because it uses more specialized code, but in addition it retains the hash table within the table object such that it can be re-used, dramatically reducing the look-up time especially for large table.
With a small vector, fmatch() is only slightly faster, but of the same order of magnitude.
library(fastmatch, warn.conflicts = FALSE)
small_vec <- c("a", "b", "x", "m", "n", "y")
length(small_vec)
#> [1] 6
bench::mark(
"base" = match(c("x", "y"), small_vec),
"fastmatch" = fmatch(c("x", "y"), small_vec)
)[1:5]
#> # A tibble: 2 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 base 1.17µs 1.24µs 738223. 2.8KB
#> 2 fastmatch 1.09µs 1.14µs 816851. 2.66KBBut, with a larger vector, fmatch() is orders of magnitude faster! ⚡
large_vec <- c(rep(c("a", "b"), 1e4), "x", rep(c("m", "n"), 1e6), "y")
length(large_vec)
#> [1] 2020002
bench::mark(
"base" = match(c("x", "y"), large_vec),
"fastmatch" = fmatch(c("x", "y"), large_vec)
)[1:5]
#> # A tibble: 2 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 base 20.19ms 20.83ms 48.0 31.4MB
#> 2 fastmatch 1.07µs 1.11µs 847431. 0BWe can also look at the hash table:
fmatch.hash(c("x", "y"), small_vec)
#> [1] "a" "b" "x" "m" "n" "y"
#> attr(,".match.hash")
#> <hash table>Additionally, fastmatch provides equivalent of the familiar infix operator:
library(fastmatch)
small_vec <- c("a", "b", "x", "m", "n", "y")
c("x", "y") %in% small_vec
#> [1] TRUE TRUE
c("x", "y") %fin% small_vec
#> [1] TRUE TRUEQ3. List four functions (not just those in base R) that convert a string into a date time object. What are their strengths and weaknesses?
A3. Here are four functions that convert a string into a date time object:
base::as.POSIXct("2022-05-05 09:23:22")
#> [1] "2022-05-05 09:23:22 UTC"
base::as.POSIXlt("2022-05-05 09:23:22")
#> [1] "2022-05-05 09:23:22 UTC"
lubridate::ymd_hms("2022-05-05-09-23-22")
#> [1] "2022-05-05 09:23:22 UTC"
fasttime::fastPOSIXct("2022-05-05 09:23:22")
#> [1] "2022-05-05 09:23:22 UTC"We can also compare their performance:
bench::mark(
"as.POSIXct" = base::as.POSIXct("2022-05-05 09:23:22"),
"as.POSIXlt" = base::as.POSIXlt("2022-05-05 09:23:22"),
"ymd_hms" = lubridate::ymd_hms("2022-05-05-09-23-22"),
"fastPOSIXct" = fasttime::fastPOSIXct("2022-05-05 09:23:22"),
check = FALSE,
iterations = 1000
)
#> # A tibble: 4 × 6
#> expression min median `itr/sec` mem_alloc `gc/sec`
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt> <dbl>
#> 1 as.POSIXct 30.11µs 32.26µs 30359. 0B 0
#> 2 as.POSIXlt 20.55µs 21.75µs 44952. 0B 45.0
#> 3 ymd_hms 2.27ms 2.4ms 414. 21.5KB 2.92
#> 4 fastPOSIXct 1.21µs 1.38µs 693507. 0B 0There are many more packages that implement a way to convert from string to a date time object. For more, see CRAN Task View: Time Series Analysis
Q4. Which packages provide the ability to compute a rolling mean?
A4. Here are a few packages and respective functions that provide a way to compute a rolling mean:
RcppRoll::roll_mean()data.table::frollmean()roll::roll_mean()zoo::rollmean()slider::slide_dbl()
Q5. What are the alternatives to optim()?
A5. The optim() function provides general-purpose optimization. As noted in its docs:
General-purpose optimization based on Nelder–Mead, quasi-Newton and conjugate-gradient algorithms. It includes an option for box-constrained optimization and simulated annealing.
There are many alternatives and the exact one you would want to choose would depend on the type of optimization you would like to do.
Most available options can be seen at CRAN Task View: Optimization and Mathematical Programming.
24.2 Exercises 24.4.3
Q1. What’s the difference between rowSums() and .rowSums()?
A1. The documentation for these functions state:
The versions with an initial dot in the name (.colSums() etc) are ‘bare-bones’ versions for use in programming: they apply only to numeric (like) matrices and do not name the result.
Looking at the source code,
-
rowSums()function does a number of checks to validate if the arguments are acceptable
rowSums
#> function (x, na.rm = FALSE, dims = 1L)
#> {
#> if (is.data.frame(x))
#> x <- as.matrix(x)
#> if (!is.array(x) || length(dn <- dim(x)) < 2L)
#> stop("'x' must be an array of at least two dimensions")
#> if (length(dims) != 1L || dims < 1L || dims > length(dn) -
#> 1L)
#> stop("invalid 'dims'")
#> p <- prod(dn[-(id <- seq_len(dims))])
#> dn <- dn[id]
#> z <- if (is.complex(x))
#> .Internal(rowSums(Re(x), prod(dn), p, na.rm)) + (0+1i) *
#> .Internal(rowSums(Im(x), prod(dn), p, na.rm))
#> else .Internal(rowSums(x, prod(dn), p, na.rm))
#> if (length(dn) > 1L) {
#> dim(z) <- dn
#> dimnames(z) <- dimnames(x)[id]
#> }
#> else names(z) <- dimnames(x)[[1L]]
#> z
#> }
#> <bytecode: 0x562e010a0b38>
#> <environment: namespace:base>-
.rowSums()directly proceeds to computation using an internal code which is built in to the R interpreter
.rowSums
#> function (x, m, n, na.rm = FALSE)
#> .Internal(rowSums(x, m, n, na.rm))
#> <bytecode: 0x562e09181458>
#> <environment: namespace:base>But they have comparable performance:
x <- cbind(x1 = 3, x2 = c(4:1e4, 2:1e5))
bench::mark(
"rowSums" = rowSums(x),
".rowSums" = .rowSums(x, dim(x)[[1]], dim(x)[[2]])
)[1:5]
#> # A tibble: 2 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 rowSums 823µs 1.3ms 828. 859KB
#> 2 .rowSums 819µs 1.3ms 795. 859KBQ2. Make a faster version of chisq.test() that only computes the chi-square test statistic when the input is two numeric vectors with no missing values. You can try simplifying chisq.test() or by coding from the mathematical definition.
A2. If the function is supposed to accept only two numeric vectors without missing values, then we can make chisq.test() do less work by removing code corresponding to the following :
- checks for data frame and matrix inputs
- goodness-of-fit test
- simulating p-values
- checking for missing values
This leaves us with a much simpler, bare bones implementation:
my_chisq_test <- function(x, y) {
x <- table(x, y)
n <- sum(x)
nr <- as.integer(nrow(x))
nc <- as.integer(ncol(x))
sr <- rowSums(x)
sc <- colSums(x)
E <- outer(sr, sc, "*") / n
v <- function(r, c, n) c * r * (n - r) * (n - c) / n^3
V <- outer(sr, sc, v, n)
dimnames(E) <- dimnames(x)
STATISTIC <- sum((abs(x - E))^2 / E)
PARAMETER <- (nr - 1L) * (nc - 1L)
PVAL <- pchisq(STATISTIC, PARAMETER, lower.tail = FALSE)
names(STATISTIC) <- "X-squared"
names(PARAMETER) <- "df"
structure(
list(
statistic = STATISTIC,
parameter = PARAMETER,
p.value = PVAL,
method = "Pearson's Chi-squared test",
observed = x,
expected = E,
residuals = (x - E) / sqrt(E),
stdres = (x - E) / sqrt(V)
),
class = "htest"
)
}And, indeed, this custom function performs slightly better8 than its base equivalent:
m <- c(rep("a", 1000), rep("b", 9000))
n <- c(rep(c("x", "y"), 5000))
bench::mark(
"base" = chisq.test(m, n)$statistic[[1]],
"custom" = my_chisq_test(m, n)$statistic[[1]]
)[1:5]
#> # A tibble: 2 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 base 1.08ms 1.1ms 859. 1.57MB
#> 2 custom 689.79µs 717.5µs 1345. 5.29MBQ3. Can you make a faster version of table() for the case of an input of two integer vectors with no missing values? Can you use it to speed up your chi-square test?
A3. In order to make a leaner version of table(), we can take a similar approach and trim the unnecessary input checks in light of our new API of accepting just two vectors without missing values. We can remove the following components from the code:
- extracting data from objects entered in
...argument - dealing with missing values
- other input validation checks
In addition to this removal, we can also use fastmatch::fmatch() instead of match():
my_table <- function(x, y) {
x_sorted <- sort(unique(x))
y_sorted <- sort(unique(y))
x_length <- length(x_sorted)
y_length <- length(y_sorted)
bin <-
fastmatch::fmatch(x, x_sorted) +
x_length * fastmatch::fmatch(y, y_sorted) -
x_length
y <- tabulate(bin, x_length * y_length)
y <- array(
y,
dim = c(x_length, y_length),
dimnames = list(x = x_sorted, y = y_sorted)
)
class(y) <- "table"
y
}The custom function indeed performs slightly better:
x <- c(rep("a", 1000), rep("b", 9000))
y <- c(rep(c("x", "y"), 5000))
# `check = FALSE` because the custom function has an additional attribute:
# ".match.hash"
bench::mark(
"base" = table(x, y),
"custom" = my_table(x, y),
check = FALSE
)[1:5]
#> # A tibble: 2 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 base 615µs 638µs 1561. 960KB
#> 2 custom 343µs 354µs 2772. 485KBWe can also use this function in our custom chi-squared test function and see if the performance improves any further:
my_chisq_test2 <- function(x, y) {
x <- my_table(x, y)
n <- sum(x)
nr <- as.integer(nrow(x))
nc <- as.integer(ncol(x))
sr <- rowSums(x)
sc <- colSums(x)
E <- outer(sr, sc, "*") / n
v <- function(r, c, n) c * r * (n - r) * (n - c) / n^3
V <- outer(sr, sc, v, n)
dimnames(E) <- dimnames(x)
STATISTIC <- sum((abs(x - E))^2 / E)
PARAMETER <- (nr - 1L) * (nc - 1L)
PVAL <- pchisq(STATISTIC, PARAMETER, lower.tail = FALSE)
names(STATISTIC) <- "X-squared"
names(PARAMETER) <- "df"
structure(
list(
statistic = STATISTIC,
parameter = PARAMETER,
p.value = PVAL,
method = "Pearson's Chi-squared test",
observed = x,
expected = E,
residuals = (x - E) / sqrt(E),
stdres = (x - E) / sqrt(V)
),
class = "htest"
)
}And, indeed, this new version of the custom function performs even better than it previously did:
m <- c(rep("a", 1000), rep("b", 9000))
n <- c(rep(c("x", "y"), 5000))
bench::mark(
"base" = chisq.test(m, n)$statistic[[1]],
"custom" = my_chisq_test2(m, n)$statistic[[1]]
)[1:5]
#> # A tibble: 2 × 5
#> expression min median `itr/sec` mem_alloc
#> <bch:expr> <bch:tm> <bch:tm> <dbl> <bch:byt>
#> 1 base 1.08ms 1.11ms 889. 1.28MB
#> 2 custom 408.58µs 428.39µs 2312. 586.98KB24.3 Exercises 24.5.1
Q1. The density functions, e.g., dnorm(), have a common interface. Which arguments are vectorised over? What does rnorm(10, mean = 10:1) do?
A1. The density function family has the following interface:
dnorm(x, mean = 0, sd = 1, log = FALSE)
pnorm(q, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
qnorm(p, mean = 0, sd = 1, lower.tail = TRUE, log.p = FALSE)
rnorm(n, mean = 0, sd = 1)Reading the documentation reveals that the following parameters are vectorized:
x, q, p, mean, sd.
This means that something like the following will work:
But, for functions that don’t have multiple vectorized parameters, it won’t. For example,
pnorm(c(1, 2, 3), mean = c(0, -1, 5), log.p = c(FALSE, TRUE, TRUE))
#> [1] 0.84134475 0.99865010 0.02275013The following function call generates 10 random numbers (since n = 10) with 10 different distributions with means supplied by the vector 10:1.
rnorm(n = 10, mean = 10:1)
#> [1] 8.2421770 9.3920474 7.1362118 7.5789906 5.2551688
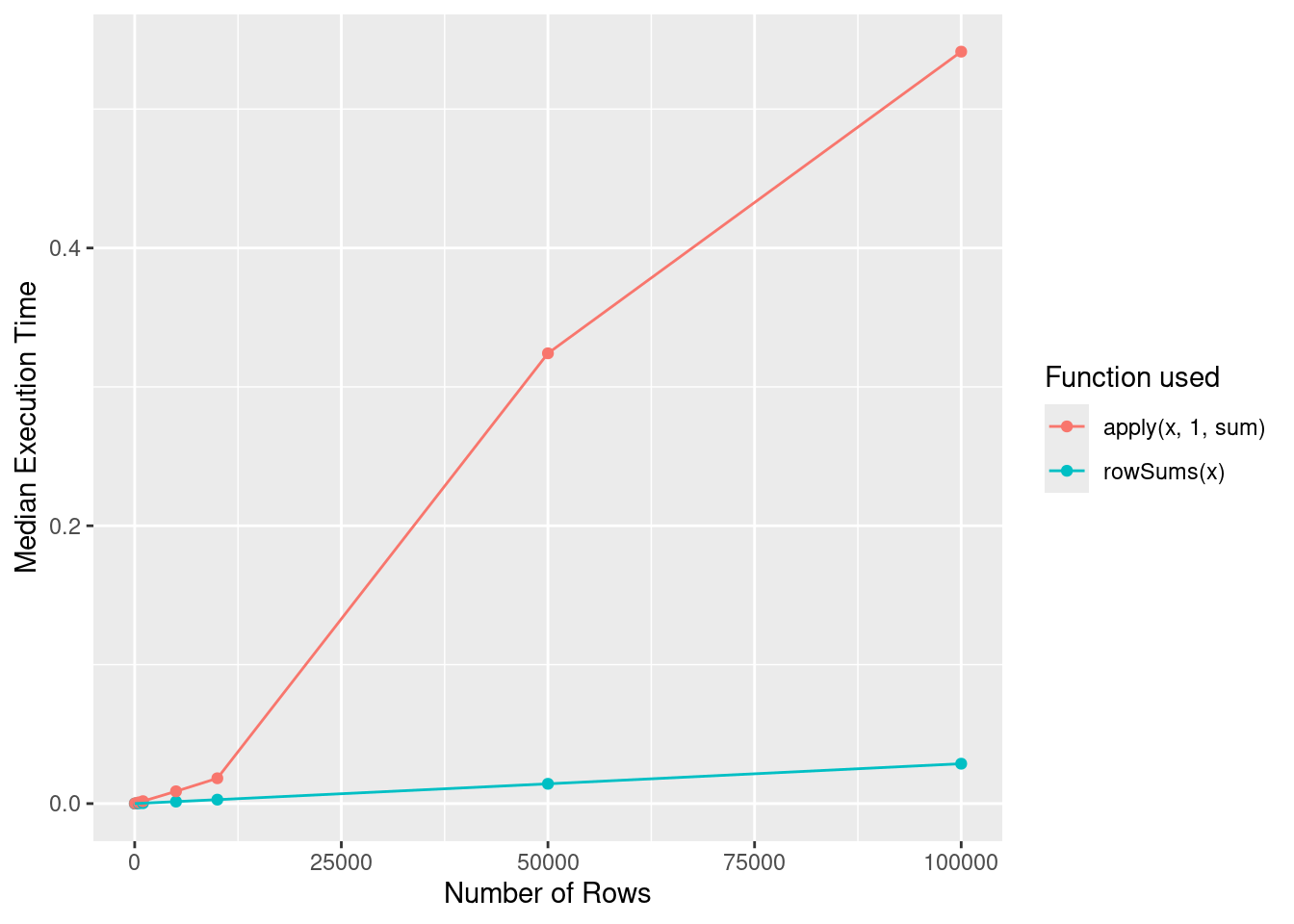
#> [6] 6.0143714 4.6147891 1.1096247 2.8759129 -0.6756857Q2. Compare the speed of apply(x, 1, sum) with rowSums(x) for varying sizes of x.
A2. We can write a custom function to vary number of rows in a matrix and extract a data frame comparing performance of these two functions.
benc_perform <- function(nRow, nCol = 100) {
x <- matrix(data = rnorm(nRow * nCol), nrow = nRow, ncol = nCol)
bench::mark(
rowSums(x),
apply(x, 1, sum)
)[1:5]
}
nRowList <- list(10, 100, 500, 1000, 5000, 10000, 50000, 100000)
names(nRowList) <- as.character(nRowList)
benchDF <- map_dfr(
.x = nRowList,
.f = ~ benc_perform(.x),
.id = "nRows"
) %>%
mutate(nRows = as.numeric(nRows))Plotting this data reveals that rowSums(x) has O(1) behavior, while O(n) behavior.
ggplot(
benchDF,
aes(
x = as.numeric(nRows),
y = median,
group = as.character(expression),
color = as.character(expression)
)
) +
geom_point() +
geom_line() +
labs(
x = "Number of Rows",
y = "Median Execution Time",
colour = "Function used"
)
Q3. How can you use crossprod() to compute a weighted sum? How much faster is it than the naive sum(x * w)?
A3. Both of these functions provide a way to compute a weighted sum:
x <- c(1:6, 2, 3)
w <- rnorm(length(x))
crossprod(x, w)[[1]]
#> [1] 15.94691
sum(x * w)[[1]]
#> [1] 15.94691But benchmarking their performance reveals that the latter is significantly faster than the former!